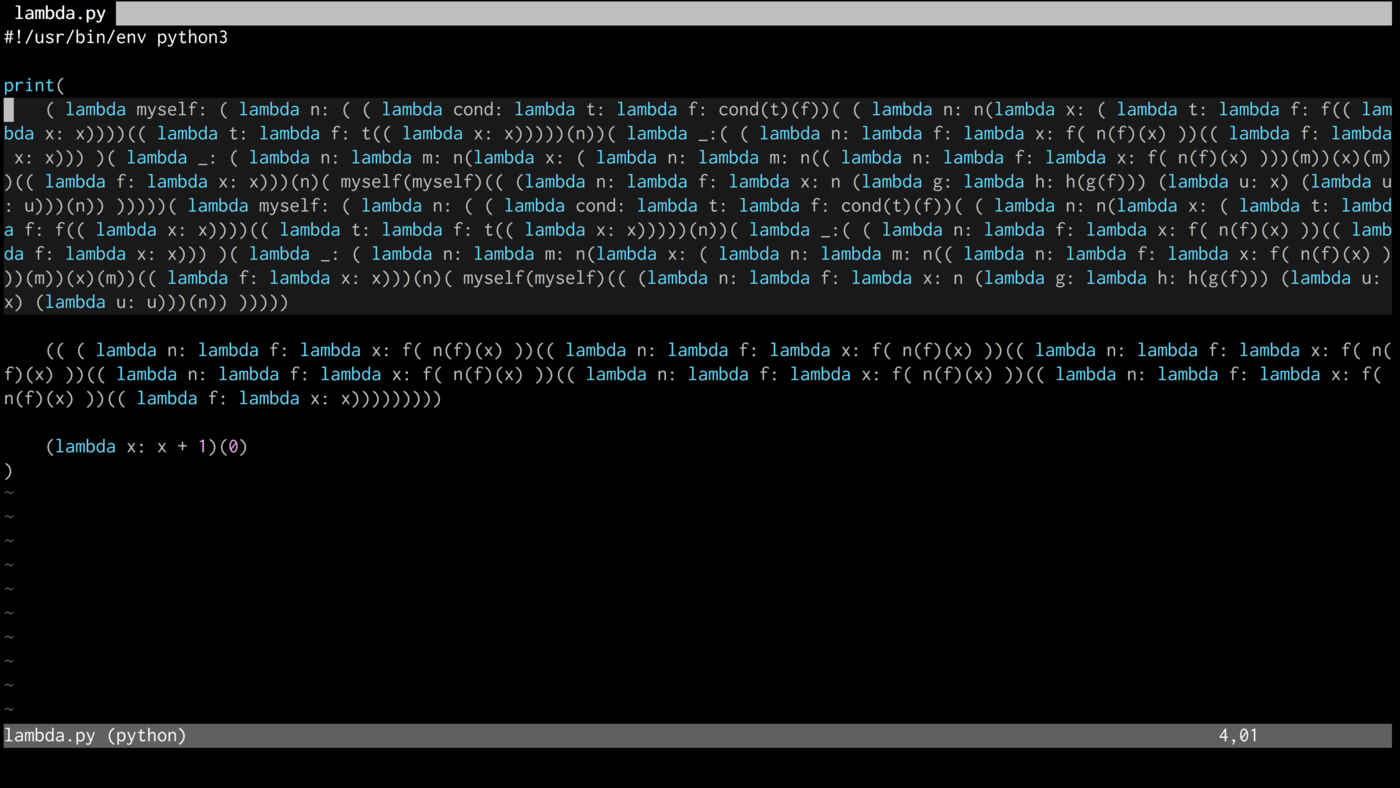
We build numbers from scratch using nothing except functions of one argument returning other functions of one argument. Those numbers, together with a similar implementation of booleans, allow us to remove all Python dependencies from the factorial function. When we're finished, it doesn't even look like code any more, but it still performs the same computation that the original Python function did. The final code is available on GitHub, but it won't make sense unless you've watched the screencast!
Note 1 (for after you've watched this screencast): When converting from Church numerals into Python numbers, there's nothing special about (lambda x: x + 1)(0). We could also use (lambda x: x + "A")(""), for example. In that case, the Church numeral 1 would be converted into "A"; 2 would be converted into "AA" etc.
Note 2: MULT can be written a bit more more simply as lambda n: lambda m: n(ADD(m))(ZERO), but the more complex version shown in the screencast is still correct.
Execute Program
Looking for something more interactive? Try Execute Program, an interactive learning platform from Destroy All Software LLC! It has courses on TypeScript, SQL, regular expressions, JavaScript concurrency, and more. All Destroy All Software subscriptions include full access to Execute Program, or you can subscribe to Execute Program directly.