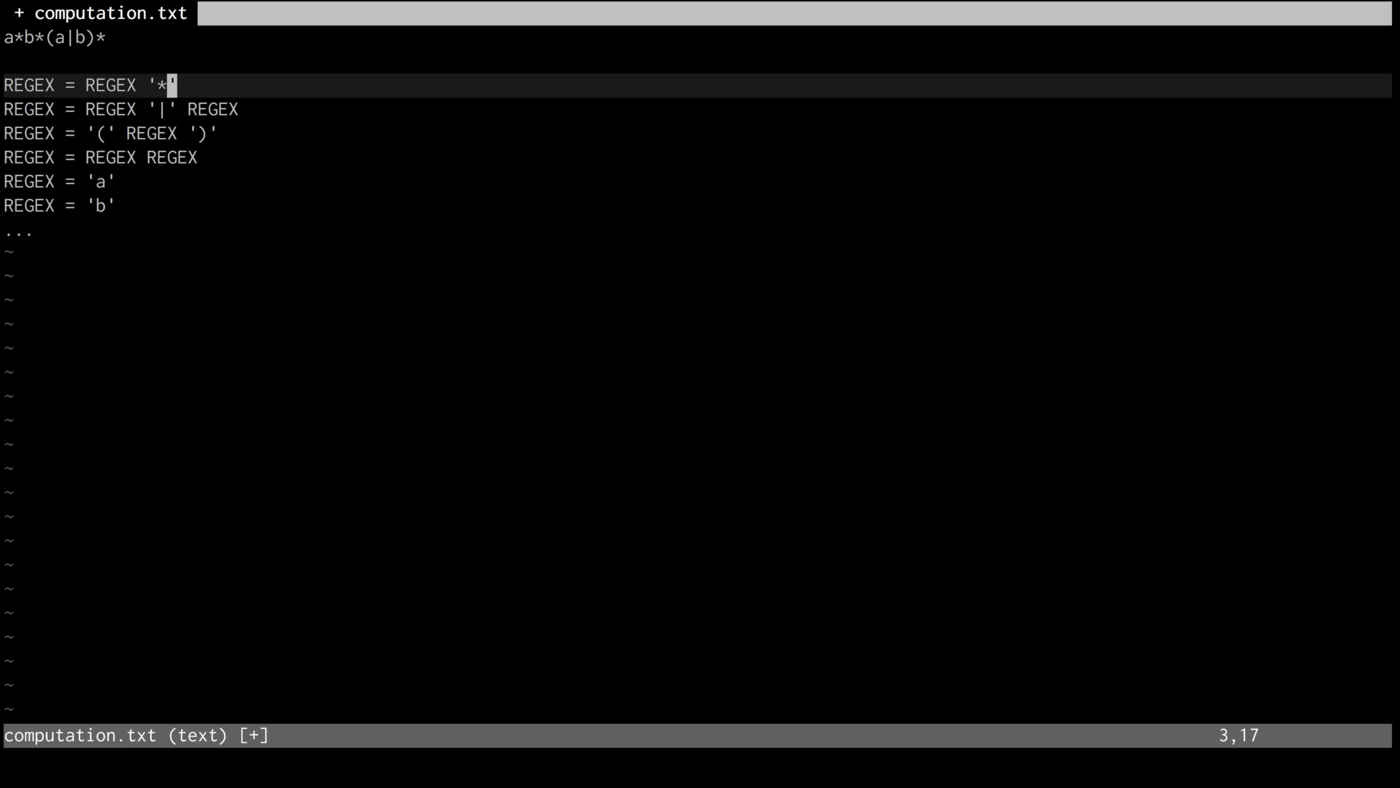
We examine some curiosities that tie the ideas in this series together. First, how can we write a grammar for the syntax of regular expressions themselves? That is, what are the rules for a valid regex? Likewise, how can we write a grammar for the syntax of grammar definitions themselves? (The answers to these are surprising!) Finally, how does the historical division between Turing machine and lambda calculus relate to the modern division between imperative and functional programming?
(Note: The grammar-grammar shown in this screencast isn't actually a grammar for itself for a trivial reason: it uses double quotes for literals, but only describes a syntax using single quotes. Changing the quotes to ''' would correct the problem, though that syntax is less clear to human readers. This doesn't impact the conclusions drawn.)
Execute Program
Looking for something more interactive? Try Execute Program, an interactive learning platform from Destroy All Software LLC! It has courses on TypeScript, SQL, regular expressions, JavaScript concurrency, and more. All Destroy All Software subscriptions include full access to Execute Program, or you can subscribe to Execute Program directly.